金曜日は休みます。次の営業は5月20日(土)です。
5月19日(金)は休みます
営業案内
23.05.17

変わり種
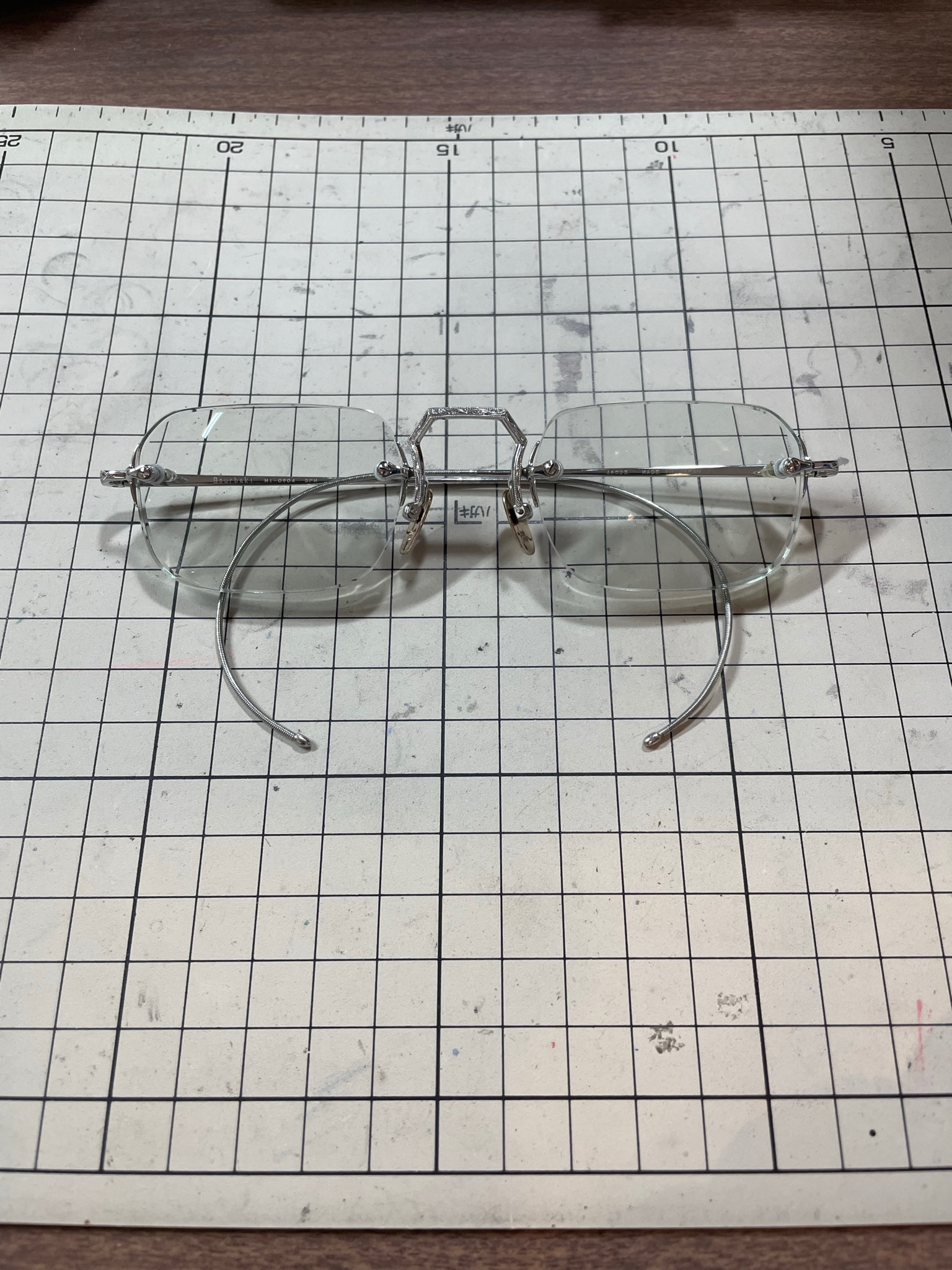
ヴィンテージのメガネ
23.05.17
お持ち込みでした。アメリカの“WELSH”って書いてあります。

セーフティメガネなんですけど、これは一味違いました。面白いフレームです。

蝶番とフロントの間に、板バネを挟んで一緒にカシメています。

初めて見たときは、蝶番が浮いているのかなと思いましたが、板バネが見えているだけです。バネがビヨンビヨンするので、フロント側に空隙が作ってあります。


ペルソールっぽい掛け心地です。これは欲しいなあとか思いながら、パッド足の取り付けと枠入れしていました。
おじさんの日々
雑記
23.05.10
4月からランニングを再開するにあたり、ちゃんとしたプロセスで靴を買ってみようと思いまして、陸上競技専門店で買ってみたんですよね。それまでは量販店で何となく柔らかくてそこそこ安い物を購入していましたけど。
それで初めて幅まで計測して頂きました。そのときに幅も甲の高さもめっちゃありますねみたいなことを言われました。その時は、まあそうなんだなぁくらいで終わり、いつもの普通の幅の靴をいつも通りのサイズ感で買いました。
結局のところ幅がわかったところで、幅を合わせる概念があんまり無いですよね。メガネでいうブリッジ幅みたいな感じでしょうけど。
それからしばらく経って、アシックスのオンラインで足の計測が出来るので、昨日ちょいとやってみました。自分で足の写真を撮るんですけど、それがこのあいだの実測値となかなか近くて驚きました。誤差5ミリ以内だったはずです。
幅の値も出るんですけど、「あなたの足の幅は平均よりとても広めです」という診断が出て、やっぱり「とても」なんだなと実感しました。
アシックスは幅も選べるモデルが何種類かありまして、ちなみにエクストラワイドでいつものスニーカーサイズよりマイナス1.5センチの診断が出ました。そんなん言われたら、それを履いてみたいなーってなりますね。
元ネタに近づける
無垢のメガネ(925silver,サンプラチナ,木)
23.05.07
サンプラチナのツーポです。自分用です。度数を変えたので、これもレンズ交換をしました。最近続いた、緑の10パーセントでツーポイントメガネを作るという流れを自分用にも適用です。お客さんのを作っていたら、自分用にも欲しくなりました。

ついでに玉型変更です。
元々はボストンとティアドロップの間みたいな玉型で横幅46ミリでした。どうしようかなと悩みまして、元ネタに近づけつつ、元ネタよりレンズは小さくしてみました。レンズ横幅48ミリです。

なんとなく細長いの掛けたくなってきたので。メガネ的Y2Kといえば細長いフレームですよね。80年代のダンヒルのフレームをベースに、30年代のアメリカっぽいフレームのディテールを加えて、さらにサンプラチナに手彫りで装飾して、でも天地浅めで2000年っぽいみたいな、色々な要素が盛りだくさんで詰め込んで破綻する寸前みたいな感じが、それがけっこう良い感じなのではと思っています。

黒セルへの鼻盛り
修理とメンテ
23.04.29
ルノアの鼻盛りしました。
昨年、当店で枠入れしており、やっぱりまつ毛がレンズ後面についちゃうよねってことで、今度は鼻盛りしました。
幅はあまり変えずに高さだけ出したいので、外側いっぱいに取り付けて、はみ出した部分は削るとこんな感じです。


細くて華奢な感じを邪魔せずに盛れたかなと思っています。鼻盛りの主張が強いと、鼻!!って感じのメガネになっちゃいますからね。

バージョン違い
無垢のメガネ(925silver,サンプラチナ,木)
23.04.29
ヴィンテージの金張りのフレームに施されている、ボシュロムのダイヤ柄を手彫りで再現してもらいました。

これは元ネタ。
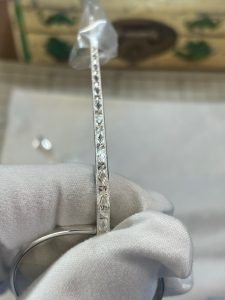
これが手彫りの再現です。銀無垢のメガネに施しました。
違いの部分は、ブリッジのセンターをどうしよう問題がありまして、元ネタは朝日っぽいシンボルが真ん中に来ます。

トップ画像と比べてみてください。今回はセンターシンボル抜きでお願いして、※みたい部分がセンターにきました。それも良いですね。
2・4・5は確定です
営業案内
23.04.28
5月2日(火)は、月例の眼科さん出張のため休みです。
5月4日(木)は、定休日です。
5月5日(金)は、色々あって休みです。

ツーポの枠入れ
ヴィンテージのメガネ
23.04.28

お持ち込みツーポの枠入れ。一般的に、30年代の〜と言われている金張りのフレームです。この前インスタにも載せたものですね。



フレームからレンズ掴みが表と裏と2本、レンズを挟む形で伸びているタイプです。掴みの裏側にネジがきってあります。レンズの厚みに影響を受けますし、そもそも保持するために挟む意味ないやーんってなって、今の形式になったんだと思います。
一発どこかで枠入れがしてありまして、そのときに右腕のネジがプラスに変えられていました。この手のフレームの初期のネジは、マイナスの溝が浅かったりネジの頭が脆かったり、加工しているときにアレコレありますから、仕方が無いと思います。


元はこんな感じでした。
すでにネジが1本変わっちゃっているのなら、こちらも思い切れるということで、美観を良くする為に現行のネジに総取っ替えしております。汎用のネジで、それっぽいのがちょうどあります。それに変えることで見た目のみならず樹脂ワッシャーとかナットとか、緩みにくくさせる手段が格段に増えます。相当実用的になります。
テンプルの閉じが微妙に合わないのが気になりましたが、智の部分が左右で形が違いますし、開いてテーブルタッチテストをしてみて、左右レンズと左右テンプルの4点で接地しているなら、この辺は追い込まない方が吉だと考えています。形状を整える過程でメキッと逝くかもしれないですから、フレームの変更は何やかんや言いつつも最小限です。
玉型変更とのことで、手元にあるAOの細長い八角形をもとに製作しております。せっかくのヴィンテージですし、アメリカで揃えてみました。
緑の10%の濃さのレンズです。ガラスのショーケースのこんな感じの雰囲気が足されるので、ツーポに緑レンズはいつ見ても綺麗だなと思います。レンズの濃さ10%の緑なら、正面はほとんど透明に見えます。


サーモント枠入れ
ヴィンテージのメガネ
23.04.28
サーモントの枠入れでした。amorのお持ち込み。
枠入れとなりますとなんともこれは大変で、リムの前面にも後面にも眉毛パーツが掛かっています。例えばフレームが出来立てホヤホヤで、眉パーツのセルがピンピンな当時なら目をつむってしまい、レンズとそれが干渉しようが御構い無しに枠入れをするということも考えられます。ただそれが製造から50年ほど経った現在となりますと、目を逸らすわけにはいきません。レンズと眉毛パーツが干渉し合えば、眉毛パーツ留めのネジ穴付近から亀裂が入りやすくなります。加工の理想像としましては、レンズと一切干渉させず、眉毛パーツの見た目通り、フレームに乗せるだけということになります。眉毛パーツは添えるだけです。



当時の精度なのか意識の問題なのか判然としませんが、とりあえず眉毛パーツがリム側に被さった原因は、眉の取り付け位置が左右非対称です。比べますと、右レンズはリムにかかり、左レンズはほとんどリムにかかりません。原因が分かったところで、フレームのカーブが強いこと(7カーブくらい)、今回の処方のレンズが左右とも単性であることを考慮して、眉毛パーツの前面は削らないことにしました。リムにかかる部分だけ眉毛パーツの前面を削ると、完成を正面から見たときに眉毛パーツの形がモロに左右非対称になってしまうので。まず後面で何とかします。
例えば、処方が強めの凹レンズの場合、ベースカーブが1とか2とかほぼ平らに上がってくると思います。レンズ端の厚みがあるため薬研のデザインで、ある程度は薬研のカーブをフレームカーブに近づけることも可能です。それをやると、今度はレンズの端っこが眉毛の前面に当たります。

なんやかんやありますけど、完成はこんな感じです。

後ろをキッチリ合わせました。リムにはみ出していたのは右レンズ側でしたが、左レンズ側もちょっとだけ綺麗に整えております。
それでは枠入れしていきます。


薬研位置は限界まで前側にして、レンズの厚みは全て後ろに持っていきました。とりあえず綺麗に入ったので安心しました。
眉毛パーツを付けたり外したり、アレコレ干渉し合っている状態で行うと、ネジに変なテンションがかかっている為に、真っ直ぐ入らなくてネジ穴を壊したり、ドライバーがなめてフレームやレンズを傷つけたりします。


この辺の段取りをしておくと、ネジがスッと入っていくのでドライバーも逃げにくく、最終の仕上がりも綺麗になります。
明日は休みます
営業案内
23.04.25
明日4月26日(水)は休みます。
何時に店に着けるのか、今のところちょっと分からないのに加えて、加工が詰まり気味の為です。
次は金曜日に開けます!





